cirklen

  

Om keglesnit.

  


start   snit    locus    ligning   refleksion    eksempler    cirkel    ellipse    parabel    hyperbel    links 
 

   








 

 

  

Cirklen som keglesnit

Keglesnittet er en cirkel hvis planet er vinkelret på keglens akse.  Hvis planet snitter keglen i spidsen er snittet et punkt.

Størrelsen af cirklen afhænger af hvor planet ligger, og hældningen af keglens sider i forhold til aksen.

         

 
    På figuren til højre kan du ændre højden af det skærende plan, og keglens vinkel.  Den cirkel der vises er den cirkel, snittet vil resultere i.

 

  

     Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

 

  
    Cirklen som geometrisk sted.

(Ryk i det hvide punkt)

Den geometriske definition af en cirkel er alle punkter, der er lige langt fra et givent punkt (centrum).

Det betyder at en cirkel er nemt at konstruere med simple midler - en snor, en pind og et stykke kridt, for eksempel.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

 

  
    Cirklens ligning

Ligningen på cirklen får vi fra Pythagoras sætning.

Hvis centrum for cirklen er (0, 0) er det meget nemt.

Når du rykker punktet P rundt i første kvadrant kan man se det retvinklede trekant, hvor radius er hypotenusen, og længden af kateterne er lig med den P's koordinater. Derfor har vi

   

Det er ligningen for en cirkel, centrum (0, 0) og radius r.

(Det er enkelt at konstatere at ligningen gælder i de andre kvadranter også.)

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

 

  
    Selv med centrum i et vilkårligt punkt C (a,b) er det ikke vanskeligt.

Hvis a og b sættes til 0 får vi den samme situation som før.

For andre værdier af a og b kan den samme retvinklede trekant ses - rykket a i x-retning, b i y-retning.

Derfor har vi:

   

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)

 
      Reflektive egenskaber

De andre keglesnit har nogle reflektive egenskaber, der bruges i teleskoper, antenner, hviskegallerier, bilforlygter og mange andre steder.  Cirklen har ikke nogen egenskaber der er umiddelbart brugelige.

Til gengæld er de årsag til en flot naturoplevelse - regnbuen.

 
 

  Regndråberne har form omtrent som en kugle (en cirkel ved alle tværsnit).

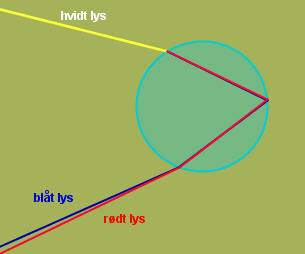
Den simple forklaring:  Lyset brydes, reflekteres fra "bagsiden" af dråben, og brydes igen på vej ud.  Resultatet er at lyset er spaltet; de forskellige farver har nu forskellige retninger, og man oplever at de kommer forskellige steder fra.  En regnbue.

Du kan læse en mere udførlig forklaring i afsnittet om regnbuen.

 

 
      Eksempler på cirkler (og kugler)

En ensartet masse, der kun påvirkes af tyngdekraft, eller kun af overfladespænding vil samle sig som en kugle.  Eksempler - næsten alle himmellegemer - måner, planeter, stjerner; regndråber.

 

 
      Bølger, der udgår fra et punkt på en overflade vil have form som cirkler (indtil de rammer noget).  Derfor er meteor kratere ringformet.

 

 
 

  En månes bane om en planet kan, hvis planeten befinder sig i midten, være en cirkel.

 
      Cirklen har altid været speciel - den perfekte figur, og derfor også egnet til kultiske formål.

 

 

  Kuplen på Peterskirken

 

Ringen;    korncirkler

 

  
 

  Cirklens egenskab - omkredsen er altid lige langt fra centrum - kan man bruge til at skubbe ting henad en flad overflade uden at løfte dem - på hjul. 

Og utallige andre anvendelsesmuligheder.

 

 

 

  

         

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)